@Phoenix, please don’t supply answers if you don’t understand the question. It’ll only get more confusing for all involved.
@7ToGo, this will involve a fair bit of maths. I put it to ChatGPT (yep, sometimes that’s the quickest way), and here’s the reply it came back with:
To calculate the 2D screen coordinates (x_screen, y_screen) of a 3D point (x, y, z) relative to a camera position and angle, you need to perform a series of transformations. Here’s a step-by-step guide:
-
Translate the Object Relative to Camera: Translate the coordinates of the object such that the camera is at the origin. This is done by subtracting the camera coordinates from the object coordinates.
( x_{\text{translated}} = x - x_{\text{camera}} )
( y_{\text{translated}} = y - y_{\text{camera}} )
( z_{\text{translated}} = z - z_{\text{camera}} )
-
Rotate the Object to Align with Camera Angle: Rotate the translated coordinates to align with the camera angle. This involves rotating the coordinates around the camera’s viewing direction.
Let’s denote the camera’s viewing direction as a unit vector ( \vec{v} = (v_x, v_y, v_z) ). Typically, this vector points from the camera towards the scene.
If your camera has a specified angle (e.g., rotation around the y-axis), you’ll need to rotate the translated coordinates accordingly.
-
Project the 3D Point onto the 2D Screen: This step involves projecting the rotated 3D point onto the 2D plane representing the screen. Typically, this involves perspective projection, which simulates how objects appear smaller as they move farther away from the viewer.
Let’s denote the position of the screen or image plane as ( d ) units away from the camera along the viewing direction.
The screen coordinates ( (x_{\text{screen}}, y_{\text{screen}}) ) can then be calculated using:
[ x_{\text{screen}} = \frac{f \cdot x_{\text{rotated}}}{z_{\text{rotated}}} + \frac{width}{2} ]
[ y_{\text{screen}} = \frac{f \cdot y_{\text{rotated}}}{z_{\text{rotated}}} + \frac{height}{2} ]
Where:
- ( f ) is the focal length of the camera.
- ( width ) and ( height ) are the dimensions of the screen.
- ( x_{\text{rotated}}, y_{\text{rotated}}, z_{\text{rotated}} ) are the rotated coordinates after the translation and rotation.
Note: The addition of ( \frac{width}{2} ) and ( \frac{height}{2} ) is to center the point on the screen. Adjust this if your coordinate system has a different origin.
-
Handle Clipping: Check if the point falls within the bounds of the screen. If the point is outside the screen bounds, you may need to clip or discard it.
This process is known as the graphics pipeline and forms the basis of rendering 3D scenes onto 2D screens in computer graphics. Keep in mind that different rendering systems might have variations in how they implement these steps, and additional considerations like field of view and aspect ratio may come into play.
A JavaScript version of this:
// Function to calculate screen coordinates
function calculateScreenCoordinates(objectX, objectY, objectZ, cameraX, cameraY, cameraZ, cameraAngle, screenWidth, screenHeight, focalLength) {
// Step 1: Translate the object relative to camera
let translatedX = objectX - cameraX;
let translatedY = objectY - cameraY;
let translatedZ = objectZ - cameraZ;
// Step 2: Rotate the object to align with camera angle
let cosAngle = Math.cos(cameraAngle);
let sinAngle = Math.sin(cameraAngle);
let rotatedX = cosAngle * translatedX - sinAngle * translatedZ;
let rotatedZ = sinAngle * translatedX + cosAngle * translatedZ;
// Step 3: Project the 3D point onto the 2D screen
let screenX = (focalLength * rotatedX) / rotatedZ + screenWidth / 2;
let screenY = (focalLength * translatedY) / rotatedZ + screenHeight / 2;
// Return the screen coordinates
return { x: screenX, y: screenY };
}
// Example usage
let objectX = 10;
let objectY = 5;
let objectZ = 20;
let cameraX = 0;
let cameraY = 0;
let cameraZ = 0;
let cameraAngle = Math.PI / 4; // 45 degrees in radians
let screenWidth = 800;
let screenHeight = 600;
let focalLength = 500;
let screenCoordinates = calculateScreenCoordinates(objectX, objectY, objectZ, cameraX, cameraY, cameraZ, cameraAngle, screenWidth, screenHeight, focalLength);
console.log("Screen Coordinates:", screenCoordinates);
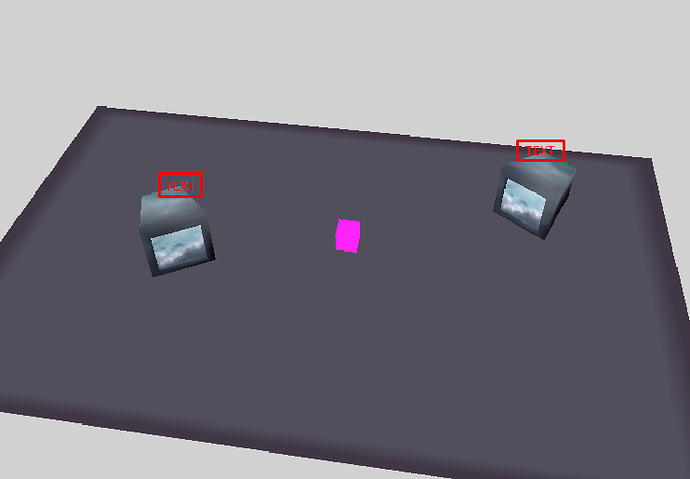




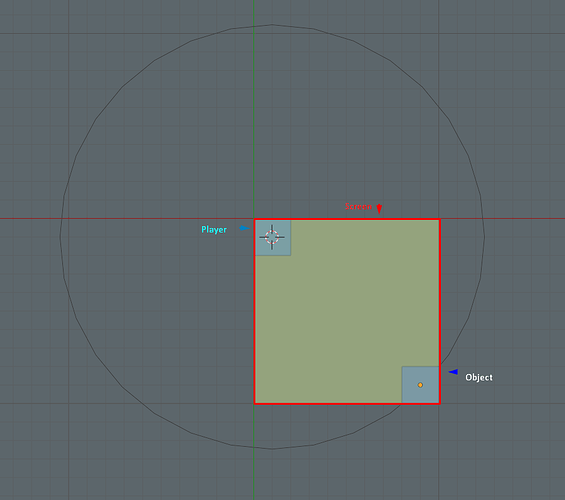
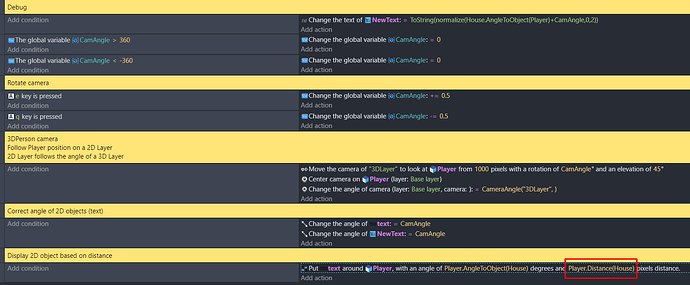
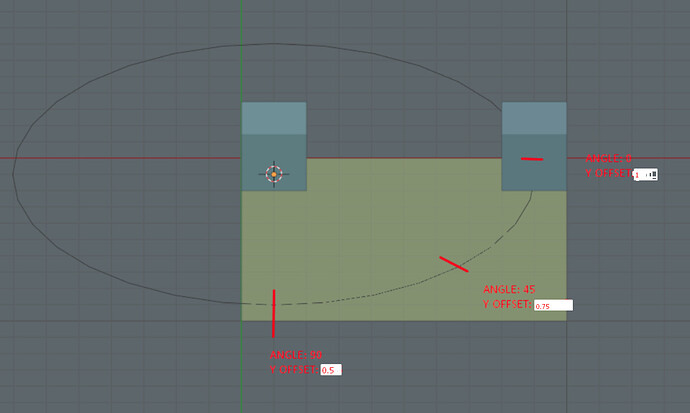


![[WIP] Overlaps objects with a 3D object in #GDevelop built-in 3D [2024/03/22]](https://img.youtube.com/vi/7UTxFPAQxME/maxresdefault.jpg)